<Index RSS Home

A Brisk Intro to Reinforcement Learning

How do humans learn? Unlike a successful image classification pipeline, humans do not require millions of labelled examples to distinguish chairs from tables. Instead, we learn by interacting with the environment, requiring no labelled supervision at all. How is this possible, and can it be replicated on a machine?

This spring I had the privilege of attending The Recurse Center in New York City and one of the topics I was keenest to explore is reinforcement learning. Reinforcement learning algorithms teach agents by letting them interact with an environment, much like humans do. What do these algorithms look like?

Monte Carlo RL: The Racetrack

Let's get up to speed with an example: racetrack driving. We'll take the famous Formula 1 racing driver Pimi Roverlainen and transplant him onto a racetrack in gridworld.


The idealised racetrack

Pimi's task is to learn how to drive from any given point on the red starting line to any point of his choice on the green finish line. He should do this as quickly as possible. We'll model Pimi's driving in a simplified way: namely as a sequence of moves from square to square. After each move he gets to accelerate by +1, 0 or -1 velocity units in either or both of the X and Y directions, giving a total of 9 possibilities(+1,+1), (+1, 0), (+1, -1), etc.. His new velocity then determines in which square he'll end up next. For safety, let's cap both the X-speed and Y-speed at 5 units.

This example is taken from the book "Reinforcement Learning" by Richard Sutton and Andrew Barto, 2018 Edition, Chapter 5.7, p111. I'll be referring to this book frequently and absolutely recommend it as an introduction to reinforcement learning.

We can write down our task using more formal terminology. Our task is to learn the best possible action in the given state we're in. In this case, a state is one of this possible cells in the grid and at each cell there's 1 of 9 possible actions we can choose from. In other words, we have to learn an ideal policy, an ideal mapping from states to actions. Again:

On such an easy course, this is an easy task for Pimi. So, to make things harder, we'll blindfold him so he cannot see where he's going. All he has access to is 9 success logbooks at each square in the racetrack -- so \(9N\) logbooks, where \(N\) is the number of squares in the track. Each logbook belongs to 1 of the 9 possible accelerations Pimi could make, say for example \((+1, 0)\). Then this logbook \((+1, 0)\) has a full record of the number of moves it's taken Pimi to arrive at the green line in the past starting at the current square, given that the action taken was \((+1, 0)\).

As Pimi drives with his blindfold on, he drives at random by accelerating in random directions because he can't see where he's going. He often crashes and when this happens, he takes a sip of refreshing blueberry juice, fetches a plaster or two and then starts again from a random point on the red starting line, keeping a stiff upper lip. As he does so, he crosses more and more squares, the smoke rises, the racetrack gets worn and the \(9N\) logbooks fill up. That's a lot of paper!

Once there's a fair amount of records in each of the \(9N\) logbooks, Pimi can start using them to make decisions instead of driving and crashing randomly. Each success logbook is indeed a measure of success of its corresponding action at that square in gridworld: the logbook averaging the lowest number of moves to completion should intuitively correspond to the best action. Why? Because the logbooks tell us exactly which of the 9 actions has, on average, a more desirable outcome. If for example logbook 3 corresponding to action \((+1, -1)\) averages 87 moves to completion, and logbook 2 corresponding to action \((+1, 0)\) averages 56 moves to completion, then choosing \((+1, 0)\) is measurably better than choosing \((+1, -1)\).

This intution is in fact correct and has solid theoretical underpinningsSutton and Barto, Chapters 3-5. The particular approach just outlined is an example of a class of algorithms called Monte Carlo algorithms in reinforcement learning. These algorithms learn the value of a particular action \(a\) taken at a state \(s\) by running many trials and evaluating the consequence for each trial. In our case this means letting Pimi race again and again and counting the number of moves it takes him to complete the track each time. The final value of action \(a\) at state \(s\) , denoted \(q(s, a)\), is then the average length of time to completion after that action, averaged over all of the trials. We can then use these value estimates to update our policy, our strategy for selecting actions. Pimi takes his logbooks, calculates the best move at each step and then picks that move instead of making a random choice. The learning problem thus breaks into 2 parts:

Finding an ideal policy is an iterative process, which involves repeating these steps over and over again. We start with a random policy and calculate the values of actions given this behaviour. This tells us which actions are optimal -- under our current, random behaviour -- and so we modify our policy to choose instead these better values. A subtle but crucial point here is that our value estimates are always with respect to our current policy, not the ideal policy. When we perform policy iteration, we move further towards the ideal policy because we weed out bad decisions: we avoid choosing actions which our value estimates tell us are measurably bad. But, crucially, our value estimates don't automatically give us the ideal policy. They merely point us in the right direction -- up to a point. That's why we should always distrust a bit of our value estimates when updating our policy. Value estimates tell us how we can improve the policy for short term gain. However, they don't tell us directly what is the ideal policy. Always going for the short term gain can preclude long-term, big benefits. For this reason, it's good always to explore when performing policy iteration. Exploring means making a move different to the one pointed to by our value estimates. We update our policy so that it follows the advice given by our value estimates most of the time -- this is known as exploitation -- but still select a random move sometimes. This last part is known as exploration. The exact proportion \(\epsilon\) of moves that are exploratory is a parameter in our algorithm. Different values of \(\epsilon\) may lead to different results: a better policy or faster / slower convergence to the optimum policy. As a rule of thumb, a higher value of \(\epsilon\) can lead to a better policy, but it'll take longer to find it: slower convergence. This is a tradeoff between exploration and exploitation and has the fancy name exploration-exploitation tradeoff.

These are all the components we need to implement our reinforcement learning algorithm. Here they are again:

So far the policy was a function from states to actions. We can also write it as a funcion \(\pi(a|s) := \pi(a, s)\) from state-action pairs to the real numbers. In this case we interpret the policy to be a probability distribution over \(a\) from which we can sample. It's a probability distribution and so \(\sum_a \pi(a|s) = 1 \) for all \(s\).

That's a lot of words. Here's some pseudocode to make things cleareradapted from Sutton and Barto, Section 5.4, page 101.

  1. Choose a small exploration parameter \(\epsilon\), for example 0.1
  2. Set the initial policy \(\pi\) to be the random policy
  3. Initialise our value estimates arbitrarily: set \(Q(s, a) \in \mathbb{R}\) arbitrarily for all \(a\) in \(A\), \(s\) in \(S\).
  4. Set \(\text{Returns}(s, a) \leftarrow \) empty list, for all \(a\) in \(A\), \(s\) in \(S\). These returns are the entries in our 'success logbooks'.
  5. Repeat forever:
    1. Generate an episode according to \(\pi: S_0, A_0, S_1, A_1 \ldots S_T\). This is one run across the racetrack until we hit the green finish line.
    2. \(G \leftarrow 0\)
    3. Loop for each episode, \(T=t-1, t-2, \ldots 0\)
      1. \(G \leftarrow G+1\)
      2. If the pair \((S_t, A_t)\) does not appear in \((S_0, A_0), (S_1, A_1), \ldots (S_{t-1}, A_{t-1})\):this condition gives what's called first-visit Monte Carlo. This is one variant of Monte Carlo prediction. Another is multiple visits, which does not have this extra 'if' condition.

        1. Append \(G\) to Returns\((s, a)\).

        2. \(Q(S_t, A_t) \leftarrow \) average(Returns(\(S_t, A_t\)))

        3. \(A^* \leftarrow \text{arg max}_a Q(S_t, a)\). Break ties arbitrarily.

        4. For all \(a \in A(S_t)\), where \(A(S_t)\) is the set of possible actions we can take at \(S_t\):

          \[
\pi(a|S_t) \leftarrow = \begin{cases}
    1 - \epsilon + \epsilon / |A(S_t)| & \text{if } a = A^* \\
    \epsilon / |A(S_t)| & \text{otherwise}
\end{cases}
\]

RaceTrack Implementation

I've implemented a Monte Carlo algorithm in Julia for the racetrack and here are my results:


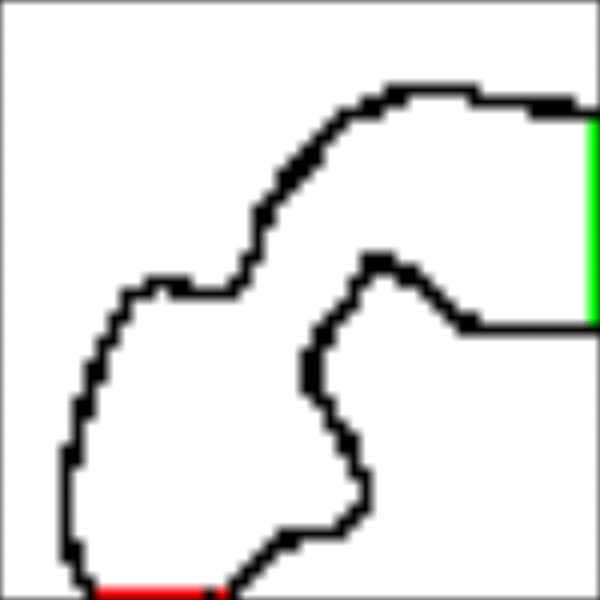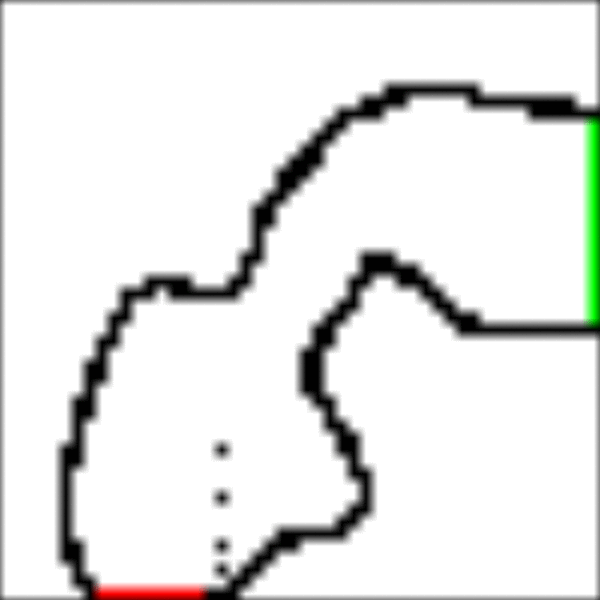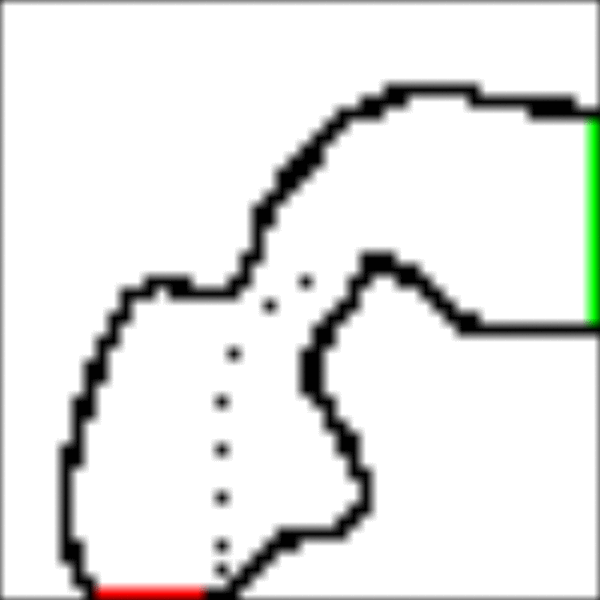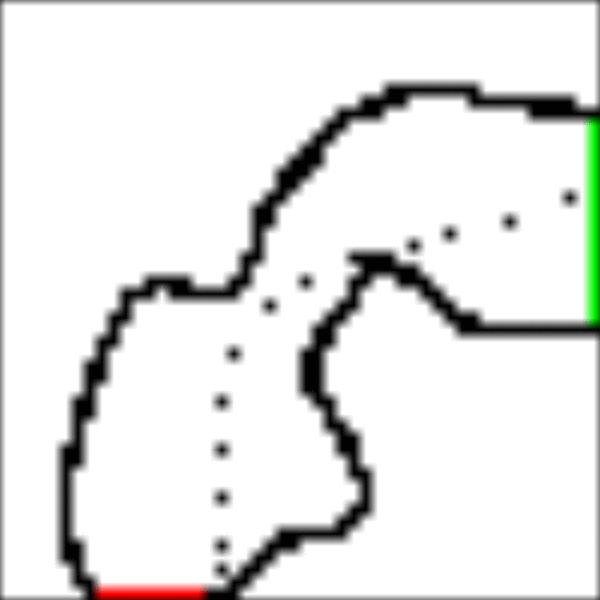
RaceTrack Result

The implementation is on GitHub and I encourage you to take a look. Let's zoom in and take a closer look at the most important parts.

"""
On-policy monte-carlo control
"""
function monte_carlo_control(track::Track, num_episodes::Int, eps::Float64)

    qval = QValues()
    returns = StateActionReturns()

    episode_lengths = []

    for i in 1:num_episodes
        episode = generate_episode(track, eps, qval)
        @assert isa(episode, Episode)
        qval = update_state_returns!(episode, eps, returns, track)
        push!(episode_lengths, length(episode))

        if i % 1000 == 0
            println(@sprintf "Done %i of %i; episode length %i" i num_episodes length(episode))
        end
    end

    return qval, episode_lengths
end

This is the heart of the algorithm: our control loop. Our policy is determined by a table of Q-Values. This is our function \(q_\pi\) from before. We populate our table by setting every entry to zero, so \(q_\pi(s, a) = 0\) for all \(s, a\). This is done by qval = QValues(). We also initialise our empty lists of returns for each state action pair returns = StateActionReturns(). Then we loop over a fixed number of episodes. In the pseudocode, this is an infinite loop. At each stage, we generate a new episode given our current qvalues: episode = generate_episode(track, eps, qval). Then we update our qvalues and our return lists: qval = update_state_returns!(episode, eps, returns track). This updates our policy.

The control loop splits into 2 core ingredients. The first core ingredient is the generate_episode function which generates an episode. The second is the update_state_returns! function which take an episode and use it to update the returns lists.

function generate_episode(track::Track, eps::Float64, q::QValues)

    episode::Episode = []
    state = random_start(track)

    for i in 1:max_episode_length
        action = epsilon_greedy(eps, q, state)
        push!(episode, (state, action))

        state = next_state(track, state, action)

        if state == TerminalState
            break
        end
    end

    push!(episode, (state, NoAction))

    return episode

end


function update_state_returns!(episode::Episode, eps::Float64,
                               r::StateActionReturns,
                               track::Track,
                               first_visit::Bool=true)

    current_return::Float64 = 0
    state, _ = episode[end]

    for i in length(episode)-1:-1:1
        if state != TerminalState && track[state.position...] == red
            current_return += -50
        else
            current_return += -1
        end
        state, action = episode[i]  

        if !((state, action) in episode[1:i-1]) || (!first_visit)
            push!(r[state, action], current_return)
        end
    end

    QValues(map(mean, r.r))
end

These 2 functions follow the pseudocode almost exactly, with the exception that in my implementation, I set an extra penalty for crashing (-50 instead of just -1). The generate_episode function relies on 2 helper functions, epsilon_greedy, which is the policy function, selecting an action given our qvalues, and next_state, which evaluates the next state given what the current state and action are and what the track shape is. I won't cover next_state here in detail. It involves checking if we've hit the boundary of the track and computing the next position given our current velocity. epsilon_greedy is quite straightforward and you can check it directly in the code.

Temporal Difference RL: Tic Tac Toe

Monte Carlo learning is simple and intuitive. To perform value prediction, we run a bunch of trials and average the returns over all these trials to obtain our estimate.

The method has a major drawback though: it takes up a huge amount of RAM. We have to store all these success logbooks which fill up as Pimi races around the track. We have to store a return for each state-action pair crossed in every episode. In fact, we rely on having a long list of returns for each state-action pair because it will increase the accuracy of our estimate. The drawback of this method is the amount of memory it requires. The greater the accuracy, the greater the memory required.

An alternative class of algorithms are temporal-difference (TD) algorithms, which we'll explore using a different example: Tic-Tac-Toe. Using a TD algorithm, we can train an AI to play Tic Tac Toe. The AI learns by playing itself.

The basic strategy is the same:

What changes is the last point: the strategy to update the value estimates. Whereas with Monte Carlo methods this required storing all of the returns following the first visit to a specific state-action pair, with TD-algorithms we have a cheaper method. Instead of storing all of the returns for every episode, we immediately update the q-values based only on the move that came immediately after the current one. So suppose when playing a game we have a sequence of states and actions \(S_0, A_0, S_1, A_1, \ldots S_T\). Then we update the q-values at \((S_i, A_i)\) thus:

\[
Q(S_i, A_i) \leftarrow Q(S_i, A_i) + \alpha [R_{i+1} + Q(S_{i+1}, A_{i+1}) -
Q(S_i, A_i)]
\]

Here \(\alpha\) is a constant parameter, and \(R_{i+1}\) is called the reward following action \(A_i\). Our returns for an episode at a given state-action pair are just the sum of rewards following that state-action pair. In the racetrack example, all of the rewards are set constant at -1, to incentivise faster runs. In my modified version there's an additional penalty for crashing because the reward is set to be -50 in that case, to disincentivise crashing. For Tic-Tac-Toe, we set the reward to be zero while the game is not finished and then:

The intuition behind this update rule is that the value will 'flow' between nodes of our state-action pair 'graph' until it reaches equilibrium. When we have equilibrium, we have the 'true' ideal value. Of course, this explanation is disappointingly vague. What's actually going on is that both Monte Carlo algorithms and TD algorithms attempt to find solutions to Bellman's equation, an equation that an idealised value functio obeying certain conditions must satisfy. I won't cover this in detail, but it's at the heart of all reinforcement learning algorithms, so be sure to check out Sutton and Barto's bookSection 3.5, page 58.

In the Tic-Tac-Toe case we can cut corners further by assigning values to states instead of state-action pairs. Whereas before we calculated a function \(Q(S, A)\) for each valid pair \((S, A)\), now we just calculate a value function \(V(S)\) for each possible state \(S\). Our policy is still \(\epsilon\)-greedy with respect to \(V\): it calculates all of the next possible states we could end up in, and selects the one with highest value \(1 - \epsilon\) proportion of times, and a random valid action the remaining times. The TD update rule then becomes

\[
V(S_i) \leftarrow V(S_i) + \alpha [R_{i+1} + V(S_{i+1}) - V(S_i)]
\]

Using state values instead of state-action values further saves the amount of storage and computation we need to do, and is perfectly valid because the desirability of a state should not change depending on how we got there. Note that this is true for the racetrack as well: we could have used state values instead of state-action values there too. The reason one cannot always do this is that general reinforcement learning policies are stochastic: the reward and next state we get back from our environment as a result of taking a certain action A from a state S can vary, even for exactly the same A and S.

I've written an implementation of a TD algorithm for Tic-Tac-Toe in Julia which you can find on GitHub.

Again we have a core training loop. Spot the updated update rule:

function play_game!(policy_me::Policy, policy_opponent::Policy)
    @assert policy_me.player == me
    @assert policy_opponent.player == opponent
    board = Board()
    current_player = opponent
    winner = nobody
    while true
        winner = get_winner(board)
        if winner != nobody
            break
        end
        if is_board_full(board)
            break
        end

        if current_player == opponent
            board = move!(policy_opponent, board)
            current_player = me
        else
            board = move!(policy_me, board)
            current_player = opponent
        end
    end

    last_index = index_from_board(board)
    update!(policy_me, last_index)
    update!(policy_opponent, last_index)
    return winner
end


function update!(policy::LearnerPolicy, last_index::Int)
    if ! policy.update
        return
    end
    if policy.exploiting_moves[end][end] != last_index
        push!(policy.exploiting_moves[end], last_index)
    end
    for moves in policy.exploiting_moves
        for i in 2:length(moves)
            a = moves[i-1]
            b = moves[i]
            policy.values[a] = policy.values[a] + policy.alpha * (policy.values[b] - policy.values[a])
        end
    end

    policy.exploiting_moves = [[]]
end

I encourage you to take a look at the full code on GitHub. There I compare training against 3 possible opponents:

The implementation takes advantage of Julia's notion of multiple dispatch which nicely allows us to compare different policies.

Using this code we can train a Tic-Tac-Toe AI which you can play in the browser:

This browser version is implemented in Elm. Check out the code on GitHub. It uses a pre-trained model that was trained using the Julia code.

Limitations of Tabular Methods

Monte Carlo algorithms and TD algorithms are both called tabular methods because computing the value function requires computing a table of values for all states, if we're computing \(V\), or state-action pairs, if we're computing \(Q\). This is OK if we have a relatively limited number of states or state-actions. In Tic-Tac-Toe, we have 2908 possible states, whereas in the racetrack example, we have \(9N\) possible state-action pairs, where N is the number of squares on the track. These numbers are still small and so tabular methods apply. But what about games like Chess or Go, which have huge amounts of states? In those cases, we cannot compute a value for every possible state or state-action pair. Instead, we approximate the value function using function approximation and machine learning. For example, the value function can be modelled to be a neural network. Different methods apply in those cases and I hope to cover them in a later blog post.

That's all, folks! For a much more comprehensive introduction to reinforcement learning algorithms, check out Sutton and Barto's book "Reinforcement Learning", 2018 Edition, which introduces the theory gradually from the ground up.

  1. (+1,+1), (+1, 0), (+1, -1), etc.
  2. Sutton and Barto, Chapters 3-5
  3. adapted from Sutton and Barto, Section 5.4, page 101
  4. this condition gives what's called first-visit Monte Carlo . This is one variant of Monte Carlo prediction. Another is multiple visits , which does not have this extra 'if' condition.
  5. Section 3.5, page 58
First published 05 October 2018 at 09:21 UTC,
last updated 05 March 2019 at 09:58 UTC.